서로 다른 단위, 서로 다른 집단의 데이터 비교하기: 표준값(z-score)

표준화란, 평균에서 떨어진 정도같이 데이터의 분포 정도를 바탕으로 데이터의 가치를 검토(비교)하기 쉽게 해주는 데이터 변환이다. 

 

표준화 공식은 다음과 같다.

표준화 공식

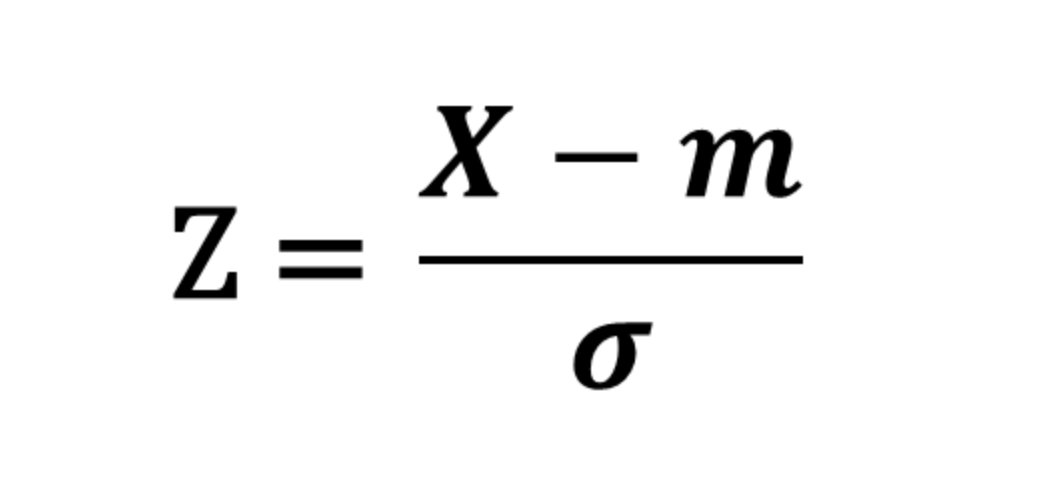
• Z = 표준값
• X = 각 데이터
• m = 평균 
• 𝜎(시그마) = 표준편차

 

평균이 0, 표준편차가 1인 표준정규분포로 환산한 것으로 표준값은 다음의 특징을 갖는다.

• z-score  = z-value = z점수 = 표준화점수 = 표준값 모두 같은 말이다.

1. 만점에 대한 기준이 달라지더라도 그 표준값의 평균은 반드시 0, 표준편차는 1이다.
   예) 100점 만점 시험과 200점 만점 시험을 서로 비교할 수 있다.
2. 단위가 달라도 그 표준값의 평균은 반드시 0, 표준편차는 1이다. 
   예) 타율과 홈런수를 서로 비교할 수 있다. 
3. 표준값이 음수이면 평균 이하, 양수면 평균 이상이다.

 

 

이를 통해 각각 다른 과목에서 동일한 점수를 받았다고 했을 때, 어느 점수가 더 가치있는지 비교할 때 표준값을 이용해서 비교할 수 있다.